radiance
density of radiant intensity with respect to projected area in a specified direction at a specified point on a real or imaginary surface 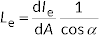
where
Note 1 to entry: In a practical sense, the definition of radiance can be thought of as dividing a real or imaginary surface into an infinite number of infinitesimally small surfaces which can be considered as point sources, each of which has a specific radiant intensity,
The equation in the definition can mathematically be interpreted as a derivative (i.e. a rate of change of radiant intensity with projected area) and could alternatively be rewritten in terms of the average radiant intensity, 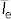 , as:
, as: 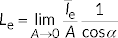
Hence, radiance is often considered as a quotient of averaged quantities; the area, 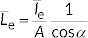 gives the average radiance and the specific measurement conditions have to be reported with the result.
gives the average radiance and the specific measurement conditions have to be reported with the result.
Note 2 to entry: For a surface being irradiated, an equivalent formula in terms of irradiance, 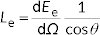 , where
, where
Note 3 to entry: An equivalent formula is 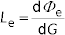 , where
, where
Note 4 to entry:
Radiant flux can be obtained by integrating radiance over projected area, 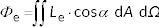 .
.
Note 5 to entry: Since the optical extent, expressed by
Note 6 to entry: The equation in the definition can also be described as a function of radiant flux, 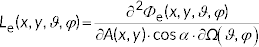
where
Note 7 to entry: The corresponding photometric quantity is "luminance". The corresponding quantity for photons is "photon radiance".
Note 8 to entry: The radiance is expressed in watt per square metre per steradian (W⋅m−2·sr−1).
Note 9 to entry: This entry was numbered 845-01-34 in IEC 60050-845:1987.
Note 10 to entry: This entry was numbered 17-1012 in CIE S 017:2011.

